怎么用Matlab解方程？
使用matlab的solve指令来解方程是一条常用的指令。
工具/材料
matlab 2016a
操作方式
- 01
打开matlab，首先界说变量x：
syms x; - 02
matlab中solve函数的格局是solve(f(x), x)，求解的是f(x) = 0的解。
第一个例子，求解最常见的一元二次方程x^2-3*x+1=0:
solve(x^2-3*x+1,x)，解出的成果用切确的根式暗示。 - 03
matlab解出的根不仅包含实根，也包含复根，例如求解三次方程x^3+1=0:
solve(x^3+1,x)
我们知道该方程有一对共轭复根，matlab也可以解出它的解。 - 04
对于超出5次（含）以上的一元函数，有时无法用solve指令求的对应的根，如下图所示。这时可以利用roots号令求解。roots号令的参数是方程的各个系数按高次幂到低次幂摆列当作的标的目的量，例如x^5+3*x^4-5*x^3+4*x^2-6*x+2=0，若是用solve指令获得的成果不克不及令人对劲，而用roots就可以获得对劲的成果。
- 05
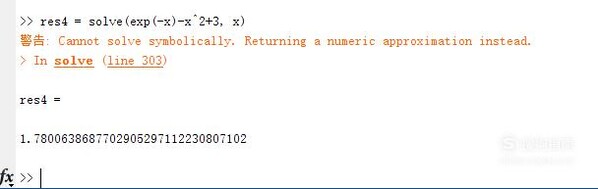
对于非多项式方程，只能利用solve求解。例如求解exp(-x)-x^2+3=0的解如下。经由过程黄色的警告可以看出，如许的方程没有解析解，与我们已知的常识不异。
- 06
最后一类方程，是一元一次方程组。这是matlab最擅长的运算，可以利用矩阵进行求解。对于齐次线性方程来讲，利用null(A,'r')。此中'r'暗示利用简化阶梯型行列式求解。对于如下的方程，可以解得线性无关的一组解。如许，我们还可以引入常量k1与k2表达通解。
- 07
对于线性非齐次的解，可以利用linsolve(A,b)。此中A是系数矩阵，b长短齐次项(若是b是多列矩阵，意味着解多个砼系数分歧齐次项的方程组)。对于图中的方程组，可已如许求解。
- End
出格提醒
matlab求解方程的方式有良多，要找到适合本身需要的方式，需要多加操练。
- 发表于 2018-02-11 00:00
- 阅读 ( 214 )
- 分类：电脑网络
